Parallel Controlled Random Search Algorithms

Introduction

With the increase in the accuracy and speed of computer simulations comes the challenge of using such simulations as a tool for the optimal design of systems and products. There has been a lot of effort in this area, such as shape optimization of airfoils and artificial heart components [5,13], and optimal design of structures for the reduction of vibrations [7].

There are a few distinctive features of a design optimization problem. The cost of evaluating the objective function can be very high, because usually the function is not given analytically, but rather defined by a ``black-box'' simulation code (such as a CFD code). In many cases the analytical derivatives are not available and numerical derivatives must be used instead. Furthermore, the function value can be subject to noise, making accurate numerical derivatives difficult to calculate. Taking these features into consideration, global direct search methods which requires no gradient information can sometimes be preferred over gradient based algorithms [4,6].

The controlled random search (CRS) algorithm for minimization is a direct search method. A number of modifications to the original controlled random search algorithm of Price [10] have been proposed [1,2,8,9,11,12]. Although direct search algorithms are robust and noise tolerant, they tend to require many more function evaluations to converge to the minimum when compared with gradient based algorithms, which can prohibit their use in design optimization, unless the algorithms are parallelised.

Unlike Genetic Algorithms (GA), the controlled random search algorithms, in their original form, do not have the same parallelism. The motivation of this work is to investigate whether parallelism could be introduced into the controlled random search algorithms by allowing multiple offsprings to be formed, and whether such parallel algorithms would be efficient.

The Parallel CRS algorithm

Algorithm PCRS(p,1,R)

• Step 1. On p processors, generate the initial population G in parallel. Let $x_l$ and $x_h$ be the points with the smallest and largest function values in G.

• Step 2. Generate m offspring using a crossover operator R on each processor.

• Step 3. Update the best and worst points $x_l$ and $x_h$.

• Step 4. Repeat from Step 2 until $f(x_h)-f(x_l)<\epsilon$.

Numerical Results

Two ``crossover'' strategies are used. The first is based on simplex [11], denoted as PCRS($p,m,\Delta$). The second is based on quadratic interpolations [2,9], denoted as PCRS(p,m,q).

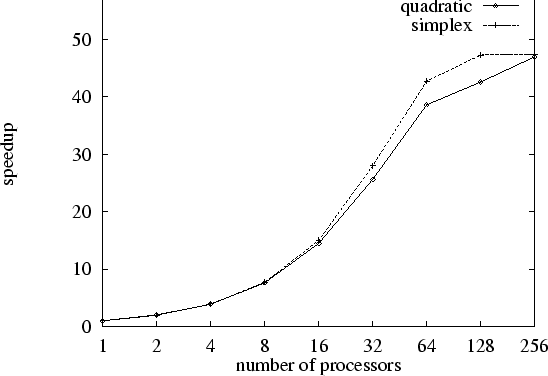
The two parallel algorithms have been tested on a set of 13 test functions on a Cray T3D parallel computer. The speedups of the parallel controlled random search algorithms PCRS(p,1,q) and PCRS($p,1,\Delta$) are plotted against the number of processors in the following figure. The speedup is defined as the number of function evalutions taken by the sequential algorithm PCRS(1,1,R), divided by that taken by the parallel algorithm PCRS(p,1,R). The parallel algorithms scale reasonably well against the number of processors for up to 64 processors. For one of the algorithms considered (PCRS(p,1,q)), the average number of function evaluations needed per processor is reduced from 667.77 on one processor to 17.31 on 64 processors, giving a speedup of 38.6. This significant reduction in the number of function evaluations makes more realistic the application of controlled random search algorithms to design optimization problem.

Figure 1:The speedup of parallel controlled random search algorithms PCRS(p,1,q) (quadratic) and PCRS($p,1,\Delta$) (simplex), against the number of processors

The parallel controlled random search algorithm has also been compared with a floating point represented genetic algorithm. In general the PCRS algorithms has been found to be more efficient.

The parallel controlled random search algorithm PCRS is available from CLIPS [3].