

Next: The State of the
Up: Other Partitioning Algorithms
Previous: Reducing the bandwidth of
Index based algorithms
In a way many of the partitioning algorithms mentioned so far
work by generating an ordered list of the vertices and bisect
this list into equal segments. In the case of spectral
bisection for example, this ordering is induced by the value of the Fiedler
vector. There are many classic ways of mapping a 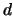 dimensional
regular grid to a one-dimensional list, such that proximate vertices
in the original grid are mapped close to
each other on the one-dimensional list.
These techniques include the Hilbert space-filling curve
[39] and the bit-interleaving transformation [66].
An irregular grid can be so indexed by embedding the grid into a
dimensional
regular grid to a one-dimensional list, such that proximate vertices
in the original grid are mapped close to
each other on the one-dimensional list.
These techniques include the Hilbert space-filling curve
[39] and the bit-interleaving transformation [66].
An irregular grid can be so indexed by embedding the grid into a
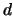 -dimensional regular grid.
The advantage of such index based methods is that the ordering can be
calculated very quickly. Index based algorithms
can also be parallelized and efficiently adopted
for situations where vertices are added or deleted as the result of
mesh adaptation. The quality
of the partitioning is comparable to that of the RCB algorithm [66].
-dimensional regular grid.
The advantage of such index based methods is that the ordering can be
calculated very quickly. Index based algorithms
can also be parallelized and efficiently adopted
for situations where vertices are added or deleted as the result of
mesh adaptation. The quality
of the partitioning is comparable to that of the RCB algorithm [66].
2000-03-21