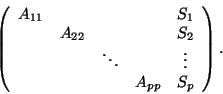
| (1) |
Y. F. Hu, K. C. F. Maguire and R. J. Blake
CSE Department, CLRC Daresbury Laboratory, Warrington WA4 4AD
Introduction
Large, sparse, unsymmetric systems of linear equations appear frequently in areas such as chemical engineering.
One way of speeding up the solution of these linear systems is to solve them in parallel. It is possible to achieve coarse-grained parallelism for the solution of unsymmetric systems, by reordering the unsymmetric matrix into bordered block-diagonal (BBD) form, and then factorizing the diagonal blocks independently [8,2,6,5].
A (single) bordered block-diagonal matrix has the following form:
The quality of reordering affects directly the parallel efficiency [6,5]. This quality is measured by the size of the border (the net-cut) and the load balance of the diagonal blocks. Since in areas such as chemical process simulation, systems of the same structure are often solved repeatedly, effort in seeking a good quality reordering can have long term pay-back [6,5].
The MONET algorithm
An efficient, high quality software for reordering large, sparse, unsymmetric matrices into BBD form has been developed [4]. The software, named MONET (Matrix Ordering for minimal NET-cut), is available on request.
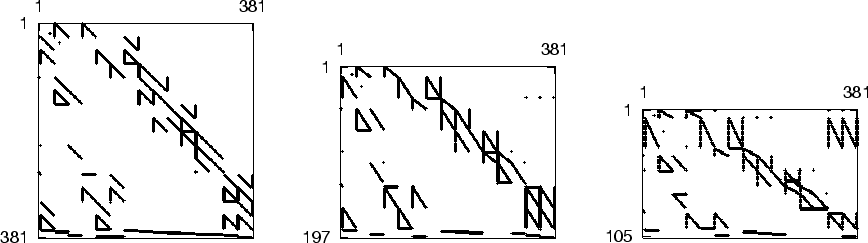
MONET is based on the multilevel approach, where large sparse matrices are coarsened into matrices of smaller and smaller sizes using a Galerkin like operator, with the prolongation operator defined by row agglomerations and column condensing. This approach is illustrated in the figure. The coarser matrices are much easier to order, yet they encapsulated the essential information of the original matrix. The coarser matrices are ordered using a Kernighan-Lin algorithm. Their ordering are inherited by the finer matrices and further refined using the Kernighan-Lin algorithm (see [4] for details)
| problem | MONET | GPA-SUM | MNC |
| lhr17 | 4/ 4.48/0.86 | 4/6.90/9.3 | |
| lhr14 | 8/ 5.31/2.70 | 8/9.01/6.0 | 6/5.40/58.8 |
| lhr11 | 8/ 7.45/0.84 | 8/9.87/6.9 | 10/9.64/148.8 |
| lhr10 | 8/ 7.19/0.07 | 8/9.59/6.0 | 10/9.65/151.6 |
| lhr07 | 16/19.38/2.06 | 16/ 18.1/11.0 | - |
| hydr1 | 4/ 2.00/8.59 | - | 4/3.43/8.8 |
| lhr04 | 4/7.75/0.07 | 4/7.85/3.4 | 3/ 6.91/49.6 |
| lns_3937 | 4/ 9.98/0.08 | 4/55.2/10.2 | 6/18.0/72.2 |
| sherman5 | 4/ 7.88/0.00 | 4/41.8/16.7 | 4/22.7/105.4 |
| west2021 | 2/ 5.54/0.05 | 2/15.0/15.3 | 3/9.25/70.6 |
| west1505 | 2/ 2.06/0.07 | 2/15.1/1.0 | 3/9.17/62.7 |
| gre_1007 | 2/12.65/0.09 | 2/34.8/3.5 | 2/ 11.8/5.9 |
| west0989 | 2/ 5.66/0.1 | 2/15.5/1.1 | 3/10.4/59.6 |
| bp_1000 | 2/15.45/0.00 | 2/20.2/6.3 | 2/ 14.1/19.0 |
MONET has been compared with two existing algorithms, namely, the MNC algorithm [2] and the GPA-SUM algorithm [1]. Two measures are used for the quality of the ordering. The first measure is net-cut, which is a measure of the size of the border, expressed here in percentage terms relative to the size of the matrix. The second measure is load imbalance, which is defined as the size of the largest diagonal block divided by the average block size, again expressed as a percentage. A good ordering has low net-cut and small load imbalance.
Table 1 compares MONET with two existing algorithms, GPA-SUM [1] and MNC [2]. The lowest net-cut is highlighted. The net-cut and load imbalance figures for GPA-SUM and MNC are taken from [1]. It can been seen that MONET gives much smaller load imbalance. In terms of net-cut, MONET is better than both GPA-SUM and MNC for most of the test cases. The number of blocks are small due to availability of data for GPA-SUM and MNC, in practice MONET can be used to reorder a matrix into any number of blocks.
Conclusion
MONET was demonstrated to give better quality ordering compared with existing algorithms, in terms of lower net-cut and smaller load imbalance. Work is underway to combine MONET with a direct sparse solver to form a parallel direct solver or preconditioner, as well as to use the underlining ordering approach for minimizing frontal size in a frontal solver.