PARALLEL EXTRAPOLATION METHOD

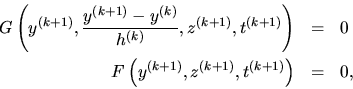
An in-house implicit Euler code (BESOLVER) of ICI Engineering was chosen as the test bed for exploring the use of parallel computers in process engineering.

The code uses the implicit Euler method to integrate equation (1). Thus (1) is discretised into (2):

$$\begin{eqnarray*} G\left(y^{(k+1)},{y^{(k+1)}-y^{(k)}\over h^{(k)}},z^{(k+1)},t^... ...right) &=&0 \\ F\left(y^{(k+1)},z^{(k+1)},t^{(k+1)}\right)&=&0,\end{eqnarray*}$$

with $y^{(k)}=y(t^{(k)})$, $z^{(k)}=z(t^{(k)})$, $t^{(k+1)}=t^{(k)}+h^{(k)}$, $t^{(0)}=t_0$ and $E(y^{(0)},t^{(0)})=0$

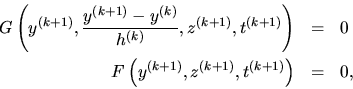
Each of the discretised equations (2) is solved using Newton's method, with the sparse systems solved using MA28 subroutines of the Harewell library. As there is yet no general sparse solver available that solves the type of sparse systems from flowsheeting efficiently on parallel computers as far as the authors understand, it is decided to explore the method parallelism. Extrapolation method is chosen because it provides some scope of parallism, and is relatively easy to be coupled into the existing code BESOLVER.

The basic idea of extrapolation method is to integrate the equation from time $t$ to time $t+H$ independently with several different step sizes such as $H$, $H/2$, $H/3$, $\ldots$, using an appropriate integration scheme (in this case the BESOLVER), and then to combine the results of all these independent integrations to get a solution at time $t+H$ of higher accuracy. Let $T_{i,1}$ denote the results of integration from time $t$ to $t+H$ with step size of $H/n_i (i=1,2,\ldots$). The extrapolation formula is then

$$T_{j,k+1}=T_{j,k}+{T_{j,k}-T_{j-1,k}\over n_j/n_{j-k}-1}.$$

The independent integrations within the extrapolation method using step lengths $H/n_i\ (i=1,2,\ldots)$ can be performed on different processors, thus parallelism across methods can be exploited in this way. However, the computational load of the parallel extrapolation method is clearly not balanced. Considering using an explicit integration scheme (such as an explicit Runge-Kutta) combined with the extrapolation method to solve an ODE, in this case the computational load on processor $i$ is proportional to $n_i$. Thus processors with smaller step length will take longer to integrate from $t$ to $t+H.$ The best speedup that can be achieved on $p$ processors, if $\{n_i\}=\{1,2,\ldots,p\}$, is roughly $(1+2+\ldots+p)/p=(p+1)/2$.

However, when an implicit scheme is used with the extrapolation method to solve the general DAE system (1), the computational load of processors is difficult to predict. A processor with a large integration step length may not necessarily has less computational load than a processor that integrates in more steps with a proportionally small step length. This is because even though the former has less nonlinear systems to solve, these nonlinear systems are generally more difficult due to the large step length, thus may require more Newton iterations per system. There are also other sources of load unbalance due to the change of step length.

The parallel implementation adopts the master-slave approach. In this approach processor $0$ is designated as the master and processor $i$ ( $i=1,\ldots,p-1$) the slaves. Slave $i$ integrates with step size $H(t)/i$ from time $t$ to $t+H(t)$ and sends the results to the master as soon as it finishes. The master uses results that are sent to it from whichever processor that has finished it integration. Once the master finds that the solution has an error below the required tolerance, it waits for the those slaves that are still integrating, but ignores the results found by them (ideally the master should interrupt these processors and ask them to stop integrating, but a suitable way of doing this was not found on the Intel. The time wasted in waiting will be reported). The master then works out the new time $t:=t+H(t)$ and new step size $H(t)$, and sends them with the solution at time $t$ to the slaves, and the above process is repeated. This parallel algorithm will be called EXEULER.

Three test cases are used to test the algorithms. Each of them models a distillation column. The number of trays, variables and equations for the three test cases are listed in Table 1.

Table 1: Table 1 Some details of the test cases which are distillation columns

number of	test case 1 (TC1)	test case 2 (TC2)	test case 3 (TC3)
trays	9	29	59
state variables	63	203	413
algebraic variables	312	872	1712
equations	375	1075	2125

The BESOLVER and EXEULER are tested on the three test cases of Table 1, on the Intel i860 parallel computers. Two integration intervals, $[t_0,t_1]=[0,1]$ and $[t_0,t_1]=[0,10]$ are used. The results of the algorithms on one of the three test cases are summarised in Table 2. The tolerance $tol$, integration interval $[0,t_1]$, elapsed time $time$ (in seconds), wasted time $time_w$ (in seconds), number of integration steps on the master $nsteps$ (including rejected steps, each step on the master consists of $i$-steps on slave $i$, $i=1,\ldots,p-1$), average order $\bar k$, error of the final solution $error$, are reported in the tables.

Table 2: Results of using BESOLVER and EXEULER on test case one

$tol$	$t_1$	time	$time_w$	nsteps	$\bar k$	error	$t_{seq}$	Sp
BESOLVER
1.0E-1	1.0	9.81	-	81	-	4.18E-3	-	-
1.0E-2	1.0	45.19	-	702	-	4.59E-4	-	-
1.0E-3	1.0	323.79	-	7048	-	4.96E-5	-	-
1.0E-4	1.0	17826.96	-	389584	-	2.54E-6	-	-
1.0E-1	10.0	13.92	-	100	-	2.18E-6	-	-
1.0E-2	10.0	56.44	-	840	-	1.71E-7	-	-
1.0E-3	10.0	411.33	-	8425	-	3.65E-8	-	-
1.0E-4	10.0	35122.00	-	734055	-	5.44E-9	-	-
EXEULER on 4 processors
1.0E-1	1.0	1.80	0.57	7	2.14	6.26E-3	3.91	2.17
1.0E-2	1.0	4.66	1.20	14	2.27	5.07E-4	8.59	1.84
1.0E-3	1.0	10.43	1.05	45	2.82	5.82E-5	20.88	2.00
1.0E-4	1.0	29.54	0.90	130	2.93	1.73E-6	57.93	1.96
1.0E-5	1.0	60.96	1.47	268	2.96	1.84E-7	119.91	1.97
1.0E-6	1.0	119.29	2.31	521	2.97	2.66E-8	237.60	1.99
1.0E-1	10.0	3.08	0.79	13	2.15	2.37E-6	6.38	2.07
1.0E-2	10.0	6.34	1.32	23	2.30	1.33E-7	12.24	1.93
1.0E-3	10.0	15.65	1.01	64	2.75	2.91E-8	30.53	1.95
1.0E-4	10.0	39.89	1.21	171	2.90	3.86E-10	78.93	1.98
1.0E-5	10.0	92.72	1.64	386	2.95	3.05E-11	181.65	1.96
1.0E-6	10.0	198.45	2.65	808	2.97	3.81E-11	393.27	1.98
EXEULER on 8 processors
1.0E-1	1.0	2.73	1.60	7	2.14	8.37E-3	11.21	4.11
1.0E-2	1.0	5.32	2.16	10	2.63	8.26E-4	20.56	3.86
1.0E-3	1.0	7.59	3.12	14	3.09	1.07E-4	29.17	3.84
1.0E-4	1.0	9.92	2.53	21	4.29	2.54E-6	41.83	4.22
1.0E-5	1.0	17.55	3.58	34	4.72	2.78E-5	74.45	4.24
1.0E-6	1.0	33.33	4.96	63	5.13	2.68E-7	140.98	4.23
1.0E-1	10.0	5.29	3.16	14	2.14	1.69E-6	20.94	3.96
1.0E-2	10.0	9.10	4.66	19	2.41	1.75E-7	35.56	3.91
1.0E-3	10.0	11.61	4.83	24	2.95	3.51E-9	46.23	3.98
1.0E-4	10.0	18.61	7.04	38	3.68	8.15E-10	75.49	4.06
1.0E-5	10.0	29.72	8.99	55	4.26	2.68E-11	122.20	4.11
1.0E-6	10.0	50.26	10.16	92	4.77	5.54E-12	209.74	4.17

Speedup is defined approximately as $t_{seq}/time$, with $t_{seq}$ the time needed for sequential implementation, and given in the last columns of the table.

As can be seen from the tables, the extrapolation code is a lot faster than BESOLVER, particular for tight tolerance. The speedup predicted previously (for explicit extrapolation method on ODE's) is 2 for 4 processors (of which only 3 slave processors are integrating) and 4 for 8 processors. The speedup actually achieved is about 2 on 4 processors, and around 3 to 4 on 8 processors.

When more than 8 processors are used, the algorithm has a maximum order of over 7 and this is rarely necessary for the tolerances of practical interest. Thus the results are not shown here.