INTRODUCTION

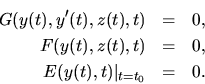
In the chemical process engineering, plant components, such as the distillation columns, are usually modeled by a set of equations. In an equation oriented approach, the following set of differential-algebraic equations (DAE's) (1) with initial values can be used to model the dynamic process flowsheeting problems.

$$\begin{eqnarray*}G(y(t),{y'}(t),z(t),t)&=&0,\\ F(y(t),z(t),t)&=&0,\\ E(y(t),t)\vert _{t=t_0}&=&0.\end{eqnarray*}$$

Where $y\in R^n$ and $z\in R^m$ are state and algebraic variables to be solved, nonlinear vector functions $G$, $F$ and $E$ are of dimensions $n$, $m$ and $n$ respectively. The system is normally stiff and sparse. To solve the problem it is necessary to integrate the system (1) up to the final time $t=t_1$ using an appropriate integration scheme. Implicit integration schemes are normally used for stability. The nonlinear equations resulted from the implicit integration scheme can be solved using Newton's method, with the sparse Jacobian systems solved using a sparse solver, such as the MA28 in the Harwell subroutine library.

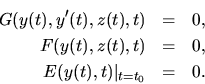
A typical process simulation problem can involve over a few thousand variables, integration of (1) over a long time period can be very computing intensive. The sizes and complexity of the problems chemical engineers can solve are thus restricted by the computing power available. Increasingly, efforts are being made to utilise the vector and parallel computers, which in theory can have a much higher peak performance than the traditional sequential computers. However, progress has been patchy (for a review see Moe and Hertzberg (1994)).

Effective use of parallel computers for the solution of systems like (1) presents a great challenge, because the initial value problems are intrinsically sequential (see [1] ). Parallelism in the solution of (1) can be roughly categorised into three sources (Bellen and Zennaro (1993)), namely parallelism across the system, parallelism across the time and parallelism across the method.

Within the process engineering community, a number of efforts have been made to investigate the effective use of parallel computers in the solution of (1). Cofer and Stadtherr (1994) investigated the use of direct sparse solver as a preconditioner for conjugate gradient type solvers. Paloschi (1994) used iterative solvers, such as the GMRES (Saad (1989)), for the solution of the sparse Jacobian systems. Skjellum (1990) and of Secchi et al. (1993) explored the waveform relaxation method and the work seems to be the most promising in the area. Parallelism across the system, rather than across the time, was actually exploited. The DAE system was partitioned and each subsystem was then solved on a processor for its assigned variables by using the approximate waveforms of other variables. This process may have to be repeated over the same time intervals for a number of times until the waveforms converge. The resulting speedup seems very promising although the method remains to be tested for more general flowsheeting systems.

So far as the authors know, there was little effort the investigation of the parallelism across the method in the flowsheeting area. It is the aim of this work thus to investigate the potential of the parallel extrapolation method.