Inertia bisection

Partitioning using coordinate bisection is susceptible to the orientation of the mesh, a simple rotation of the mesh would result in different partition. Inertia bisection [54] remedies this by using a procedure that is invariant to rotation. It finds the principal axis of the communication graph. Here the coordinates of the vertices of the communication graph are defined as explained in Section 3.1.1. If one assumes that each vertex has a unit mass associated with it, then the principal axis is the axis that minimizes the angular momentum when the graph rotates around it.

Consider a graph of $n$ vertices associated with a 3D mesh. Let the principal axis be $y_0+\alpha * y$ with $y_0$ a point in space, $\alpha$ real numbers and $y$ a unit vector. Then any vertex $i$ with coordinates $x_i\in R^3$ has an angular momentum equal to the square of its distance to the axis, or

$$\vert\vert x_i-y_0\vert\vert^2-{(x_i-y_0)^Ty\over \vert\vert ... ...vert x_i-y_0\vert\vert^2-(x_i-y_0)^Ty, \quad i = 1, \ldots , n$$

The principal axis minimizes the sum of these momentums:

$$\sum_{i=1}^n \left(\vert\vert x_i-y_0\vert\vert^2-(x_i-y_0)^Ty\right)$$

subject to $\vert\vert y\vert\vert^2=1$. It is possible to prove, using the necessary condition of constrained optimization, that $y_0=\bar x={1\over n} \sum_{i=1}^n x_i$ and that $y$ is the eigenvector that corresponds to the largest eigenvalue of the $3\times 3$ matrix

$$I=\sum_{i=1}^n (x_i-\bar x)(x_i-\bar x)^T$$ (1)

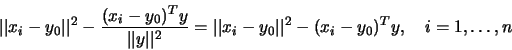
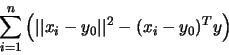
Once this eigenvector has been found, every vertex can be sorted based on its projection onto the principal axis, that is, the value $(x_i-\bar x)^Ty$, or simply $x_i^T y$.

The main computational cost of the inertia algorithm is the formation of the inertia matrix (1), which requires of the order of $O(n)$ operations. The algorithm is easy to parallelize [18,74].