Parallel multilevel
Although the multilevel approach reduces the computing time significantly, for a very large mesh it can prove to be memory intensive - often exceeding the limits of single CPU memories. Furthermore as the ultimate purpose of partitioning is for the subsequent implementation of the application code on parallel machines, it makes sense to have a parallel partitioning code. Besides, a fast parallel partitioning algorithm can also be used for the purpose of dynamic load balancing. There have been a number of efforts in this area.
Parallel multilevel recursive bisection algorithm PMRSB -
In [2,3], the multilevel spectral bisection was parallelized specifically for the Cray T3D architecture using the Cray SHMEM facility. The linear algebra algorithms (Lanczos, Rayleigh iteration and SYMMLQ) involved are easy to parallelize. Difficulties arose in the parallel graph coarsening, in particular, in the parallel generation of the maximal independent set. These were tackled by using a number of parallel graph theory algorithms from the literature. On a 256 processor Cray T3D, the resulting algorithm PMRSB is able to partition a graph of 1/4 million vertices into 256 subdomains, 140 times faster than a workstation (of similar specification to one processor of the Cray T3D) using an equivalent serial algorithm.
Parallel multilevel ![]() -way partitioner ParMETIS -
-way partitioner ParMETIS -
In [49], a parallel multilevel ![]() -way partitioning
scheme was developed. This is based on work in the sequential
-way partitioning
scheme was developed. This is based on work in the sequential
![]() -way partitioning algorithm METIS [52], but with some
interesting modification to facilitate parallelization. In particular,
as in PMRSB [2,3],
a parallel algorithm due to Luby [57]
for finding the maximal independent set was employed. However unlike MRSB,
where the maximal independent set is used directly to form the
coarse graph, here the maximal independent set is
used for a different purpose. By considering one independent set
at one time, it is possible to avoid conflicts
during the coarsening stage when the vertices are matched,
as well as during the uncoarsening stage when the boundaries are refined.
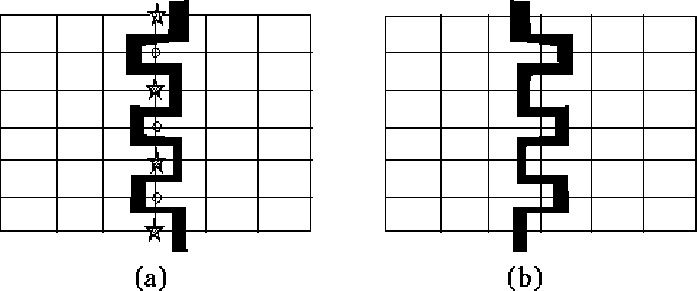
To illustrate this consider the graph of Figure 11 (a)
distributed
across two processors. Suppose one hopes to refine the partition to
reduce the edge-cut using K-L type algorithms. To do this in parallel
without proper scheduling, processor one finds all the vertices
that have a positive gain if moved to processor two (those
marked with a star), and sends them to processor two;
likewise processor two
sends all the vertices marked with a circle to processor one.
This results in the graph shown in Figure 11 (b)
which has the
same edge-cut of 13.
Any subsequent use of the K-L
algorithm in parallel would result in an oscillation
between these two graphs. This situation is a result of the fact that
moving vertices marked with a star to processor two affects the gains
of those marked with a circle, therefore the moves should not be
carried out in isolation. One way of avoiding this
conflict is for the two processors to communicate
with each other and to collaborate on a migration strategy.
When there are more than two processors, this may necessitate
a coloring of the processor graphs so that processors are grouped
in pairs and refinement is carried out on boundaries of the
paired processors [18].
-way partitioning algorithm METIS [52], but with some
interesting modification to facilitate parallelization. In particular,
as in PMRSB [2,3],
a parallel algorithm due to Luby [57]
for finding the maximal independent set was employed. However unlike MRSB,
where the maximal independent set is used directly to form the
coarse graph, here the maximal independent set is
used for a different purpose. By considering one independent set
at one time, it is possible to avoid conflicts
during the coarsening stage when the vertices are matched,
as well as during the uncoarsening stage when the boundaries are refined.
To illustrate this consider the graph of Figure 11 (a)
distributed
across two processors. Suppose one hopes to refine the partition to
reduce the edge-cut using K-L type algorithms. To do this in parallel
without proper scheduling, processor one finds all the vertices
that have a positive gain if moved to processor two (those
marked with a star), and sends them to processor two;
likewise processor two
sends all the vertices marked with a circle to processor one.
This results in the graph shown in Figure 11 (b)
which has the
same edge-cut of 13.
Any subsequent use of the K-L
algorithm in parallel would result in an oscillation
between these two graphs. This situation is a result of the fact that
moving vertices marked with a star to processor two affects the gains
of those marked with a circle, therefore the moves should not be
carried out in isolation. One way of avoiding this
conflict is for the two processors to communicate
with each other and to collaborate on a migration strategy.
When there are more than two processors, this may necessitate
a coloring of the processor graphs so that processors are grouped
in pairs and refinement is carried out on boundaries of the
paired processors [18].
 |
An alternative coloring strategy is however used
in [49], as it is believed that
pairing the processors lacks the global view of the
sequential ![]() -way partitioning where each vertex
is free to move to the subdomain that leads to the
maximum reduction in the edge-cut.
-way partitioning where each vertex
is free to move to the subdomain that leads to the
maximum reduction in the edge-cut.
The new strategy is based on coloring the vertices
in a number of colors. Vertices of the same color
form an independent set.
Each colored vertex set is considered one at a time
when doing the refinement. By the definition
of an independent set (Section 3.4.2),
no two vertices
in the set are linked by an edge, therefore
moving a vertex in this colored independent set
to another processor does not affect the gain of other vertices
of the same color.
Consequently, each processor may decide to
send vertices which it identifies as
having a positive gain, without the need to communicate with
other processors,
knowing that such a gain will be realized. This procedure
can be repeated on vertices of each color in turn.
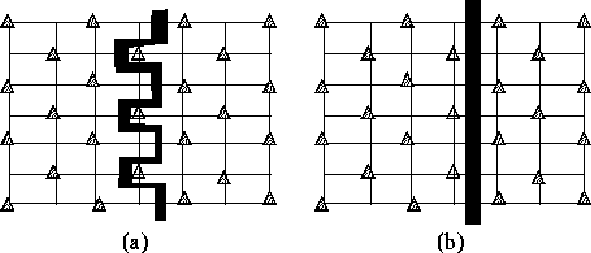
Using this strategy Figure 12 (a) is colored
using two symbols (either with or without a ![]() ).
When applying K-L refinement on vertices colored with
).
When applying K-L refinement on vertices colored with ![]() ,
Figure 12 (a) becomes
Figure 12 (b), which has a smaller edge-cut
of 7, instead of the original edge-cut of 13.
,
Figure 12 (a) becomes
Figure 12 (b), which has a smaller edge-cut
of 7, instead of the original edge-cut of 13.
 |
The resulting parallel algorithm was implemented on a Cray T3D using its SHMEM communication facility [49]. Table 1 [49] gives a rough idea of the capability of the algorithm and its performance in relation to PMRSB [3]. The two algorithms were applied on two meshes, 598a (a 3D finite element mesh of 144649 nodes and 1074393 edges) and MDUAL (the dual graph of a 3D finite element mesh, with 258569 vertices and 523132 edges). ParMETIS is significantly faster and gives smaller edge-cut. The scalability of both approaches is similar with approximately three to four fold improvement in performance as the number of processor elements (PEs) is increased by a factor of eight.
A coarse grained modification
suitable for MPI implementation was introduced more recently [50].
In this version, the vertex coloring is not used to avoid
the need for global point to point communication when each color
is considered during the coarsening and refinement phase.
Graph folding to part of the parallel processors is also
carried at coarse levels to reduce the communication.
During the coarsening
stage, each processor examines its vertices, and chooses their
heavy edge neighbors for matching. A match request of vertex ![]() with a local neighbor
with a local neighbor ![]() is granted immediately while a request for match with a remote neighbor
is granted immediately while a request for match with a remote neighbor
![]() is sent to the remote processor for consideration only if
is sent to the remote processor for consideration only if ![]() .
During the refinement phase, conflict is avoided by allowing flow
in one direction at a time. That is, a vertex
.
During the refinement phase, conflict is avoided by allowing flow
in one direction at a time. That is, a vertex ![]() belongs
to partition
belongs
to partition ![]() is considered
for moving to partition
is considered
for moving to partition ![]() only if
only if ![]() (or
(or ![]() at the next round).
Applying this strategy to Figure 12 (a), assuming that the
flow is from the right to the left, results in Figure 12 (b).
Using MPI,
this version of the ParMetis algorithm was demonstrated [50] to
lead to much better performance than that based on vertex coloring.
at the next round).
Applying this strategy to Figure 12 (a), assuming that the
flow is from the right to the left, results in Figure 12 (b).
Using MPI,
this version of the ParMetis algorithm was demonstrated [50] to
lead to much better performance than that based on vertex coloring.
Parallel multilevel ![]() -way partitioner JOSTLE-MD -
-way partitioner JOSTLE-MD -
The parallel partitioning algorithm in [83]
used a different refinement strategy to that of vertex coloring.
As this algorithm is designed also for dynamic load balancing,
the initial partitioning is assumed to be unbalanced.
For any two neighboring subdomains ![]() and
and ![]() ,
the flow (the amount of load to be migrated to achieve global
load balance) is first calculated. The flow from
,
the flow (the amount of load to be migrated to achieve global
load balance) is first calculated. The flow from ![]() to
to ![]() is denoted as
is denoted as ![]() . Let
. Let ![]() denote the total weight of the
vertices on the boundary of
denote the total weight of the
vertices on the boundary of ![]() which have a preference to migrate to
which have a preference to migrate to
![]() . Let
. Let
![]() , which represents
the total weight of all boundary vertices with a positive gain after
the flow is satisfied. Then the load to be migrated from
, which represents
the total weight of all boundary vertices with a positive gain after
the flow is satisfied. Then the load to be migrated from
![]() to
to ![]() is given by
is given by
Having decided on the amount of load to be migrated, the idea
of relative gain is then used to work out which vertices are to be migrated.
The relative gain of a vertex ![]() on processor
on processor ![]() is defined as
is defined as
![]() , where
, where
![]() denotes the gain of moving
denotes the gain of moving ![]() to processor
to processor ![]() ,
and
,
and ![]() those vertices in processor
those vertices in processor ![]() that are connected with
that are connected with
![]() .
The vertices on the boundaries are sorted by their relative gain
and a weight of
.
The vertices on the boundaries are sorted by their relative gain
and a weight of ![]() is migrated. This avoids
the collisions that arise when the gain of vertices varies. But in a situation
when each boundary vertex has exactly the same
gain, a tie break strategy is necessary. This was not detailed in
[83]. The algorithm has been shown to be very efficient
in partitioning and re-balancing the meshes resulting from
adaptive refinement. The parallel JOSTLE algorithm has been compared with
ParMETIS. It was found to give partitioning of better quality,
although it runs slower than ParMETIS [85].
is migrated. This avoids
the collisions that arise when the gain of vertices varies. But in a situation
when each boundary vertex has exactly the same
gain, a tie break strategy is necessary. This was not detailed in
[83]. The algorithm has been shown to be very efficient
in partitioning and re-balancing the meshes resulting from
adaptive refinement. The parallel JOSTLE algorithm has been compared with
ParMETIS. It was found to give partitioning of better quality,
although it runs slower than ParMETIS [85].
Other parallel graph partitioning algorithms -
In [18] a parallel single level algorithm, combining inertia bisection with K-L refinement, was implemented. Possible conflict during the refinement stage was avoided by the pairing of processors based on the edge-coloring of the processor graph. The quality of the partition was not as good as multilevel algorithms.
In [77] a spectral inertia bisection algorithm was introduced. The spectral basis set of eigenvectors for the coarsest graph was first calculated and serves as the spectral coordinates of the vertices. The graph was partitioned with the inertia bisection algorithm (Section 3.1.2), based on these spectral coordinates. Part of the algorithm was parallelized. This algorithm is also suitable for dynamic load balancing, on applications where the mesh is enriched by refining the individual elements. In such a case the refinement can be captured by updating the vertex weights of the dual graph of the mesh, without changing the graph itself. The mesh is repartitioned quickly after refinement, using the spectral information originally calculated for the top level coarse mesh. Since the size of the dual graph does not change, the repartitioning time does not change with the increase of the mesh size, as the refinement steps are carried out. However a possible disadvantage of this approach is that in order to reuse the spectral information, only the vertex weights, not the edge weights, are allowed to be updated. Thus the edge-cut may not be a good representation of the actual edge-cut of the mesh after many levels of refinement.