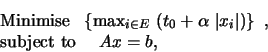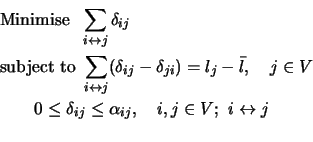

Next: Node Selection for Migration
Up: Flow Calculation
Previous: The method of potential
A possibly better model [43] of the communication cost in the migration process,
as opposed to (12),
is the maximum cost of load migration
over all processors, that is
Here 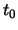 is the communication latency
and
is the communication latency
and 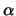 is the subsequent cost of communication per word.
The flow calculation problem then becomes
is the subsequent cost of communication per word.
The flow calculation problem then becomes
which is equivalent to
| |
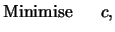 |
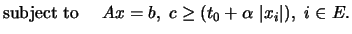 |
(15) |
However it is not clear that an efficient parallel algorithm exists for
such a linear programming problem.
Similar linear programming based flow calculation were proposed in [67],
where the problem
was solved. Here 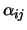 is the number of vertices on subdomain
is the number of vertices on subdomain 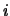 that may be
moved to subdomain
that may be
moved to subdomain 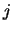 , using a node selection strategy based on layering
(see the next section). This linear programming problem was solved
using the simplex method to give the flow. The problem has
, using a node selection strategy based on layering
(see the next section). This linear programming problem was solved
using the simplex method to give the flow. The problem has
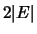 variables and
variables and 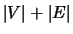 constraints. A multilevel approach was used to
group subdomains into super-partitions, thereby
breaking the linear programming problem into smaller ones to be solved
by subsets of processors. This reduced the overall complexity of
solving the linear programming problem.
constraints. A multilevel approach was used to
group subdomains into super-partitions, thereby
breaking the linear programming problem into smaller ones to be solved
by subsets of processors. This reduced the overall complexity of
solving the linear programming problem.


Next: Node Selection for Migration
Up: Flow Calculation
Previous: The method of potential
2000-03-21