The method of potential

As mentioned before, the solution of the system of linear equations (9) is not unique. The motivation of the algorithm [43], called the method of potentials here for reasons explained later, is to choose amongst these solutions one that minimizes the data movement. For this section (Section 4.3.4), the processor graph is assumed to be directed, with the direction of each edge going from the vertex with higher index to the one with lower index.

Let $A$ be the matrix associated with the linear system (9), let $x$ be the vector of $\delta_{ij}$'s and $b$ the right hand side of (9). Assuming that the Euclidean norm of the data movement is used as a measure of data movement, and that the unit communication cost between any two processors $i$ and $j$ is $1/(c_{ij})^{1/2}$. Let $W$ denote the diagonal matrix of size $\vert E\vert\times\vert E\vert$ consisting of the $c_{ij}$, then one needs to find a solution $x$ which solves the following minimization problem:

$${\rm Minimise\ \ }{1\over 2} x^TW^{-1}x,\cr {\rm subject\ to\ }\quad Ax=b.$$ (12)

Here $A$ is the $\vert V\vert\times \vert E\vert$ matrix associated with system (9). It is called the vertex-edge incident matrix [68,8] of the directed processor graph, given by

$$(A)_{ik}=\left\{ \begin{array}{rl} 1,&\qquad{\rm if\ vert... ...f\ edge\ }k,\\ 0,&\qquad{\rm otherwise}. \end{array} \right.$$

Applying the necessary condition for the constrained optimization problem (see [27]), after some algebraic manipulation, one has

$$x=WA^Td,$$ (13)

where $d$ is the vector of Lagrange multipliers given by the equation

$$L\ d \ =\ b,$$ (14)

with $L=AWA^T$.

Thus the problem of finding an optimal load balancing schedule is transformed to that of solving the linear equation (14). Once the Lagrange multipliers are found, then the load transfer vector is $x=WA^Td$.

For any graph, each row $k$ of the matrix $A^T$ only has two non-zeros, $1$ and $-1$, corresponding to the head and tail vertices of the edge $k$. Therefore the amount of load to be transferred from processor $i$ to processor $j$ (assuming $i$ is the head and $j$ the tail), along the edge $e=(i,j)$, is simply

$$\delta_{ij}=c_{ij}(d_{i}-d_{j}),$$

where $d_{i}$ and $d_{j}$ are the Lagrange multipliers associated with vertices $i$ and $j$ respectively. The quantities $d_i$ and $d_j$ can also be looked upon as the potentials at the vertices $i$ and $j$ and their (weighted) difference gives the flow between the two vertices. That is why we call this method the method of potentials.

The matrix $L=AWA^T$ is a generalized form of the Laplacian matrix (6). For many parallel computers the unit communication cost is roughly the same between any two processors ($W=I$), in which case this matrix is the same as (6).

The linear system (14) can be solved by many standard numerical algorithms. The conjugate gradient algorithm was used in [29] because it is simple, easy to parallelize and converges quickly. For preconditioning, the diagonal of the Laplacian may be used.

As a simple example, considering the processor graph in Figure 14. The load for each processor is given in brackets. The average load is 16.25 and the largest load imbalance is $(25-16.25)/16.25=53.8$%. The Laplacian system (assuming a weighting of $W=I$) is now

$$\pmatrix{ &1&-1&0&0&0&0&0&0\cr &-1&3&0&-1&0&-1&0&0\cr &0&0&2&... ...-1.25\cr -1.25\cr -1.25\cr -1.25\cr -1.25\cr -1.25\cr -1.25 }.$$

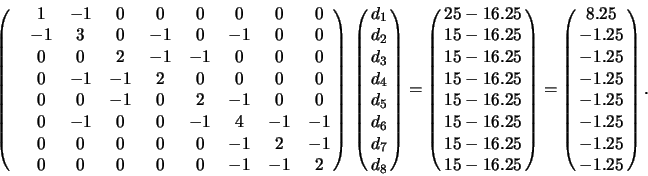
The solution of this linear equation is

$$(d_1,\ldots,d_8) =(11.28, 2.53, -2.22, -0.47, -2.72, -1.97, -3.22, -3.22).$$

These Lagrange multipliers (the potentials) are illustrated in Figure 15 in brackets. The amount of load to be transferred between two neighboring processors is the difference between their potentials, and is shown along the edges in Figure 15. For example, processor 1 needs to send to processor 2 a load of $11.28-2.53\approx 9$.

Figure 15: The potentials and the amount to be migrated along each edge

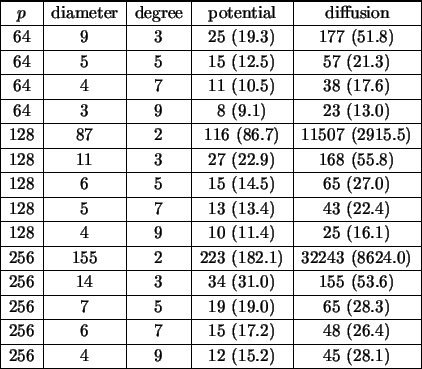
Table 2 gives the result of the method of potentials and that of the diffusion algorithm on random graphs of varying connectivity. The algorithms have been implemented on a Cray T3D with MPI. It can be seen that in general the method of potentials is faster, and that for graphs of small connectivity it is considerably faster. The same conclusion can be drawn when applying the two algorithms on processor graphs from real applications [43].

Table 2: The number of iterations (and in brackets, time for convergence, in milli-seconds) for the algorithm of potentials and the diffusion algorithm, on randomly generated graphs

Figure 16: Comparing the Euclidean norm of the flow from three algorithms: dimension exchange algorithm (top solid line), diffusion algorithm (middle broken line) and the algorithm of potentials (bottom broken line)

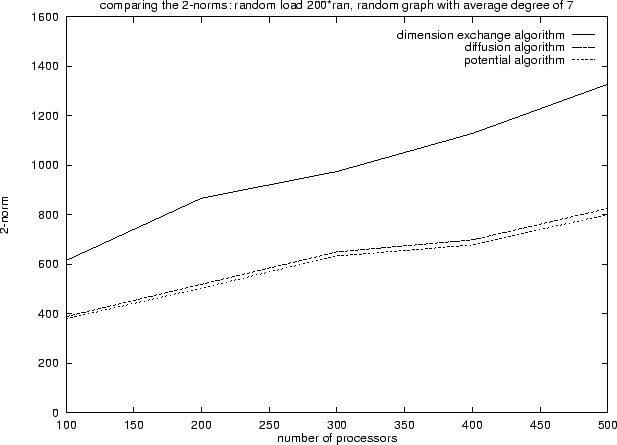When examining the Euclidean norm of migrating flow (Figure 16), it was surprising to find that the norm for the diffusion algorithm was usually as small as that for the method of potentials, and much smaller than that of algorithms such as the dimension exchange algorithm. It has now been proved [44] that diffusion type algorithms also have a minimal norm property. In fact it is possible to prove a rather general result [45] that if a flow calculation algorithm is based on the polynomial of the weighted Laplacian, $l^{(k+1)} = p_k(L)l^{(1)},$ where $p_k$ is a $k$-th order polynomial such that $p_k(0)=1$, then the flow generated, provided that the algorithm converges, solves (12). In other words, all polynomial based flow calculation algorithms, including the diffusion algorithm (11), generate exactly the same minimal flow as the algorithm of potentials, provided that the same edge weights $c_{ij}$'s are used. In terms of the rate of convergence, the algorithm of potentials is of course better. It also converges for any positive edge weights.