Flow Calculation

The problem can be formally stated as follows:

Definition     Given a graph $G=(V,E)$, let each vertex $i\in V$ have a load $l_i$ associated with it. The flow calculation problem is to find the amount of migrating load $\delta_e$ along each edge $e\in E$, such that after the migration, the load on each vertex is the same. That is

$$l_i+\sum_{j\leftrightarrow i} \delta_{ji}=\bar l, \quad i\in V.$$ (9)

Here $\bar l$ is the average load over all vertices, defined as $\bar l=(\sum_{i\in V} l_i)/\vert V\vert$, and $\delta_{ji}$ is the amount of load to be migrated from node $j$ to node $i$.

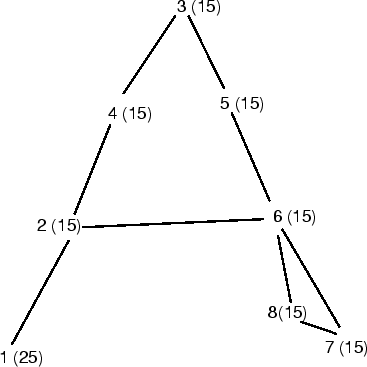
The graph here is the so called processor graph of the partitioning. Each vertex of the processor graph corresponds to a subdomain (or a processor) and two vertices are linked by an edge if the two subdomains share a boundary. Figure 14 shows the processor graph corresponding to the partitioning in Figure 13 (b). The load $l_i$ can simply be taken as the number of nodes in the subdomain $i$. Figure 14 shows that subdomain 1 has a load of 25 nodes, whilst others have 15 nodes each. In the following the terms vertex and processor are used interchangeably.

Figure 14: processor graph associated with the partitioned mesh in Figure 13 (b), and the load (in brackets) on each processor

It is noted that the flow calculation problem does not have a unique answer. This is because the solutions are given by a linear system (9), with $\delta_{ij}$ as the unknown. There are $\vert V\vert$ equations (out of these, $\vert V\vert-1$ are independent), and $\vert E\vert$ unknowns. As there are usually more edges than vertices in a graph (that is, $\vert E\vert>\vert V\vert$), there are usually more unknowns than equations and so the answer to the problem is not unique.

This flow calculation problem has been studied by many authors [4,6,14,28,43,44,41,78,88,89]. Apart from parallel unstructured mesh based applications, it has appeared in areas such as parallel molecular dynamic simulation [7,55]. Some of the algorithms are discussed in the following.