I have research interest in the following areas:

Natural Language Processing

Human written language can be very nuanced. This is especially true when the written text is twisted to avoid detection, which is the case when applying NLP to detect hate speeches. In order to detect hate speech with high performance, we have to apply adversarial learning techniques to find words that sounds the same as hateful ones, but spelled differently, or are scrambled and manipulated to avoid detection by typical ML algorithms, but can still be recognized by human. On the other end of the spectrum, I found human names are very well formed and we can easily detect the gender and nationality/ethnicity from names alone.

Machine Learning & Visualization

Visualization can be considered unsupervised machine learning, because the goal of visualization is to discover patterns in the data without labels, exactly the same as the goal for unsupervised machine learning. This seamless connection between machine learning and visualization means that techniques from one area can help to solve problems in another. For instance, we can use SVD and convex optimization to improve graph visualization, or use the multilevel approach successful in visualization to DeepWalk, a graph dimension reduction algorithm in machine learning. This alleviates the tendency of DeepWalk to be trapped in a local minimum on very large graphs, and improves its performance overall.

Understanding Human Sense of Aesthetics

Can we understand and characterize the human notion of beauty? This is the ultimate goal of a joint project with Ohio State University (Prof. Hanwei Shn and his student XIaoqi Wang). We are using generative adversarial networks (GAN) to generate visual representations of graphs that are predicted to be aesthetically appealing to humans, and the results are very promising. Long term, I would like to create a generator that takes data as input, and automatically generates a visualization that not only reveals the intrinsic structure and anomalies of the data, but is also pleasing to look at and easy for our end users to understand.

Recommender Systems

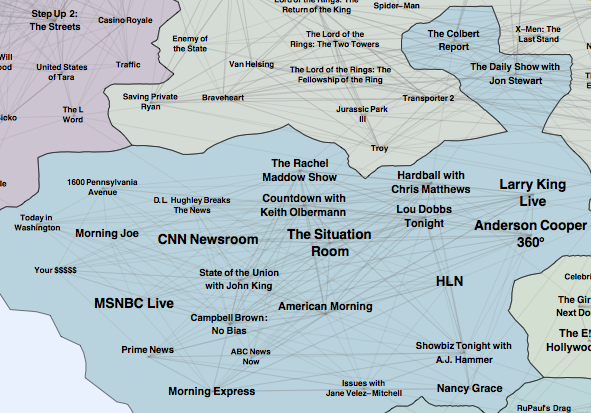
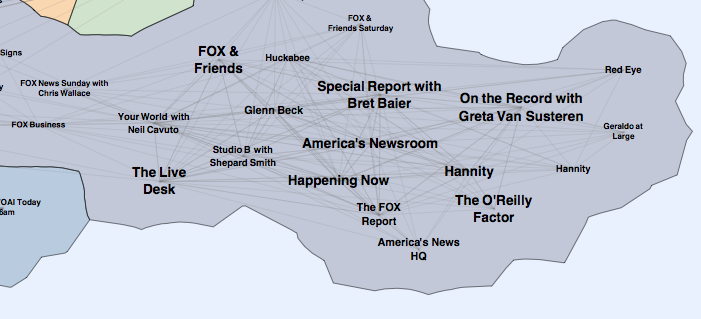
A common task of recommender systems is to improve customer experience through personalized recommendations based on prior implicit feedback. These systems passively track different sorts of user behavior, such as purchase history, watching habits and browsing activity, in order to model user preferences. Unlike the much more extensively researched explicit feedback, in our application we do not have any direct input from the users regarding their preferences. In particular, we lack substantial evidence on which products consumer dislike. We proposed an algorithm treating the data as indication of positive and negative preference associated with vastly varying confidence levels. This leads to a factor model which is especially tailored for implicit feedback recommenders. We also suggest a scalable optimization procedure, which scales linearly with the data size. In addition, we offer a novel way to give explanations to recommendations given by this factor model. A paper describing this work is here . The algorithm is used successfully within a recommender system for an IPTV service for millions of users. Here is a visualization of the Map of TV based on the recommender system.

big data mining and visualization

The many endless rivers of text now available present a serious challenge in the task of gleaning, analyzing and discovering useful information. I developed a system, TwitterScope, that streams, stores, clusters and visualizes tweets related to any keywords of interest. This search engine is available internally to AT&T users. A public version which monitors a set number of topics are at http://tibesti.research.att.com/twitterscope/. A paper is here.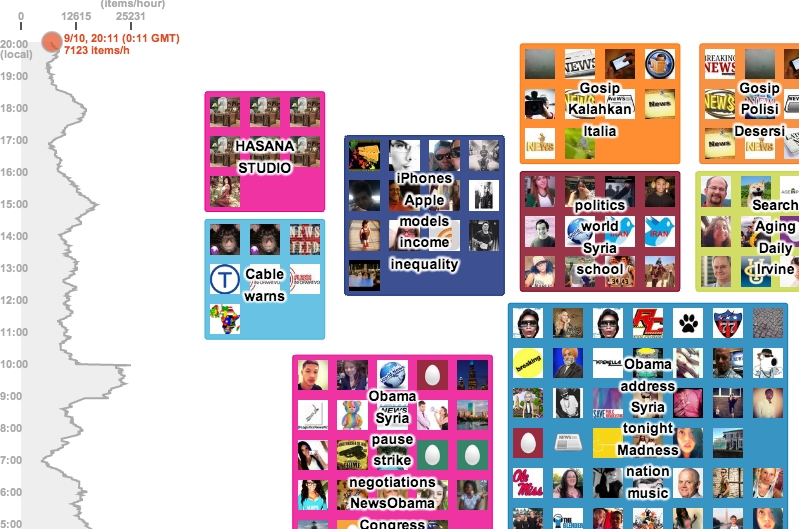

network/graph analysis and visualization

Networks or graphs encapsulate complex relations in many application areas. Algorithms to analysis these networks, for example, in finding out community structures/clusters, calculating PageRank, and visualizing the networks, play an important role in discovering structures and gaining knowledge from complex data. A novel multilevel force directed algorithm with fast force calculation using octree data structure and supernode force approximation was proposed and implemented, resulted in an efficient graph drawing algorithm with a complexity of O(|V| log(|V|) + |E|). This algorithm can handle graphs of millions of nodes, as well as large tree like graphs, such as the Mathematics Genealogy Trees.

The resulting software, sfdp, is available in GraphViz .

Sometimes, the conventional node-link diagram is not sufficient, not cognatively appealing, for representing information contained in the data. GMap is a technique that visualize relational data as maps. A paper is here. Some maps..

One interesting problem is node overlap removal. Often nodes contain information that need to be displayed. Traditional graph drawing algorithm ignore the node size. An efficient and effective overlap removal algorithm, PRISM, has been developed.

Figure: An illustration of the PRISM overlap removal algorithm.

Edge bundling is a technique that can help in reduce clutters of large graph visualization.

numerical linear algebra

I have been doing research and developing software in AMG, iterative algorithms and geometric multigrid. A parallel AMG code SAM (Scalable Algebraic Multigrid) has been developed.

dynamic load balancing

 For many practical applications, such as adaptive mesh based calculations, the load changes during the course of parallel computation, making it necessary to balance the load dynamicly, and in parallel. Most of the existing parallel dynamic load balancing algorithms involve two steps: flow calculation and migration. The traditional algorithm for flow calculation is the diffusion algorithms. We have proved that this type of algorithms are "optimal" in terms of the amount of load migration. However we have proposed a new algorithm which is also "optimal", but is much more efficient.

static load balancing (grid partitioning)

the numerical solution of partial differential equations usually involves dividing up the physical domain into small elements or volumes to form a mesh. To solve the problem on a distributed memory parallel computer, the mesh should be decomposed into subdomains, the number of which usually equals the number of processors, with each subdomain assigned to a unique processor. The static load balancing problem is that of how to decompose the mesh into subdomains so that each processor has about the same amount of computation and so that the communication cost between processors is minimized, with the overall aim of minimizing the runtime of the calculation.
Figure: mesh around a car body partitioned into 16 subdomains.

sparse matrices ordering I

solving general nonsymmetric sparse systems in parallel efficiently is a challenging problem. One way of achieve that is to order the system into bordered block-diagonal form, and factorize the diagonal blocks in parallel. A multilevel algorithm MONET has been develop for this purpose. Other ordering algorithms are also being investigated, for example, for minimizing frontal size/bandwidth in the context of frontal/multifrontal solvers.
Figure: A sparse matrix ordered into BBD form with two diagonal blocks.

sparse matrices ordering II

The problem of reordering a matrix to minimize its front size has many applications. A good reordering helps to reduce the memory usage as well as floating point operations of a frontal solver, it also helps when forming incomplete a LU factorization as a preconditioner for Krylov subspace iterative algorithms. We have proposed a multilevel algorithm for reordering sparse symmetric matrices to reduce the wavefront and profile. The algorithm uses a maximal independent vertex set for coarsening and the Sloan algorithm on the coarsest graph. It is shown to produce orderings that are of a similar quality to those obtained using the best existing combinatorial algorithm (the hybrid Sloan algorithm), yet does not require any spectral information and is significantly faster, requiring on average half the CPU time. A paper entitled Multilevel algorithms for wavefront reduction is available for download.

Figure: mesh around the skirt of a rocket partitioned into 16 subdomains.

numerical optimization

I have been working on interior point algorithms for linear and nonlinear optimization. I am also interested in global optimization algorithms (Genetic Algorithms, a parallel controlled random search algorithm). I implemented

CFD solvers

research and development in solvers for CFD, particularly for finite volume/finite element based calculations. These include FAS nonlinear multigrid for SIMPLE based finite volume imcompressible calculations, block correction based parallel multigrid linear solver and AMG solvers for DNS.

Figure: agglomeration based multigrid -- mesh coarsening.

parallelising industrial finite element applications

FLITE3D is a multigrid Euler code for external aero-dynamics. It is used extensively by British Aerospace in aircraft design and simulation. This code has been efficiently parallelised in the FLITE3D project. It has been used for production since and has been proved highly robust and efficient.

density distribution around an F18 as iterations evolve, calculated using FLITE3D on a Cray T3E/900.

chemical process simulation (Parallel DAE solvers)

chemical processes are frequently simulated using a large set of differential algebraic equations (DAEs). Computer simulation of such chemical processes involves integration of DAEs over the time interval of interest. Implicit integration schemes are normally used for stability. The nonlinear equations resulted from the implicit integration scheme can be solved using Newton's method, with the sparse Jacobian systems solved using a (direct) sparse solver, such as the MA48 in the Harwell subroutine library. This can be extremely computing intensive. Increasingly, efforts are being made to utilise the vector and parallel computers. Effective use of parallel computers for the solution of DAEs presents a great challenge, because the initial value problems are intrinsically sequential, and the components of the solution process, such as the direct sparse solver, are not easily parallelised either. One way of introducing parallelism into the sparse solver is through reordering the matrices into special for for parallel factorization. To this end we have developed the MONET software . Alternative approaches have also been explored, including iterative algorithms with suitable preconditioners. On a more coarse grain level, parallel extrapolation method has been investigated. It has been demonstrated that some speedups can be achieved.