A Gallery of Large Graphs
graph visualization of matrices from the University of Florida Collection
Graph visualization is a way to discover and visualize structures in complex relations. What sort of structures are people who do large scale computation studying? We can get a glimpse by visualizing the thousands of sparse matrices submitted to the University of Florida Sparse Matrix collection using sfdp algorithm . The resulting gallery contains the drawing of graphs as represented by 2568 sparse matrices in this collection. Each of these sparse matrices (a rectangular matrix is treated as a bipartite graph) is viewed as the adjacency matrix of an undirected graph, and is laid out by a multilevel graph drawing algorithm. If the graph is disconnected, then the largest connected component is drawn. The largest graphs have tens of millions of nodes and over a billion of edges. A simple coloring scheme is used: longer edges are colored with colder colors, and short ones warmer. The graphs are in alphabetical order. Use the "Search" link to find graphs of specific characters.
Prev 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 All Next Search
JGD_Homology/n3c4-b3 |
JGD_Homology/n3c4-b4 |

JGD_Homology/n3c5-b1 |
JGD_Homology/n3c5-b2 |

JGD_Homology/n3c5-b3 |

JGD_Homology/n3c5-b4 |

JGD_Homology/n3c5-b5 |

JGD_Homology/n3c5-b6 |

JGD_Homology/n3c5-b7 |
JGD_Homology/n3c6-b1 |
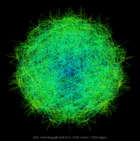
JGD_Homology/n3c6-b10 |
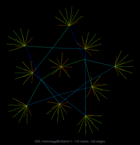
JGD_Homology/n3c6-b11 |
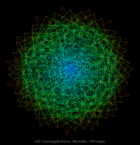
JGD_Homology/n3c6-b2 |
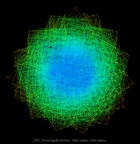
JGD_Homology/n3c6-b3 |
JGD_Homology/n3c6-b4 |
JGD_Homology/n3c6-b5 |
JGD_Homology/n3c6-b6 |

JGD_Homology/n3c6-b7 |
JGD_Homology/n3c6-b8 |
JGD_Homology/n3c6-b9 |
Prev 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 All Next Search