Dynamic Load Balancing Algorithms

When adaptive algorithms are used, after an interval of computation, the mesh may be refined (or coarsened) at some locations, usually based on an estimate of the discretization error. The refinement (or coarsening) process can generate widely varying numbers of mesh nodes on the processors. Subsequently, there is a need for dynamic load balancing. Load imbalance may also be caused by the use of local time stepping, local spatial approximation schemes of varying orders [26], or non-linear material properties.

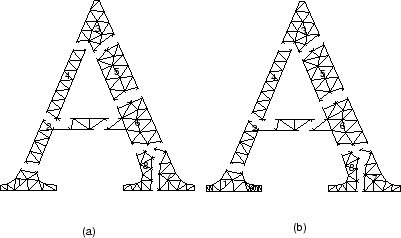
As a simple example, Figure 13 (a) shows a mesh of shape ``A'', partitioned into 8 subdomains. It has been refined in Figure 13 (b). Due to the mesh refinement subdomain 1 has more nodes than the other subdomains.

Figure 13: (a) A mesh of ``A'' shape partitioned into 8 subdomains; (b) the mesh refined at subdomain 1

In general dynamic load balancing algorithms should satisfy the following objectives

• Re-balance the load of each processor with speed and scalability.
• Minimize the edge-cut (or more precisely, the communication cost of the application after the re-balance)

In order to satisfy the first objective, the dynamic load balancing algorithm should not only identify what to migrate efficiently, the amount of data required to be migrated should also be kept to a minimum. Various metrics such as TotalV and MaxV [70] have been used to model and minimize the data migration cost.

One way to re-balance the load is to repartition the mesh using one of the partitioning algorithms of Section 3. Indeed parallel algorithms such as JOSTLE or ParMETIS are able to partition large mesh very rapidly [83,70]. For example, ParMETIS was able to partition a mesh of the order of 1 million nodes in less than 2 seconds on 128 PEs of a Cray T3D [70]. However it is important, but difficult, to ensure that the new partitioning will be ``close'' to the original partitioning. Should the new partitioning deviate considerably from the old one then the cost of transferring large amounts of data will be incurred. It has been found that repartitioning is more appropriate when there has been a substantial localized refinement on the mesh [72,5].

An alternative strategy is to migrate the excessive nodes to neighboring processors, effectively shifting the boundaries to achieve a balanced load. This approach may potentially cause less movement of data than repartitioning, although the edge-cut after the migration could possibly be larger than that given by a global repartitioning. Therefore care must be taken to keep edge-cut down when choosing the nodes to be migrated. It has been found [72] that this strategy is more suitable when the load imbalances caused by the refinement are low, or when localized high imbalances occur throughout the mesh. This is because in such cases the optimal partition will be relatively close to the initial partition.